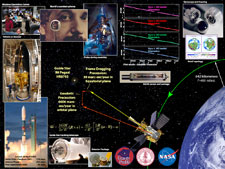
Overview of the GP-B Mission

Mission Objectives

Gravity Probe B (GP-B) is a NASA physics mission to experimentally investigate Albert Einstein's 1916 general theory of relativity—his theory of gravity. GB-B used four spherical gyroscopes and a telescope, housed in a satellite orbiting 642 km (400 mi) above the Earth, to measure in a new way, and with unprecedented accuracy, two extraordinary effects predicted by the general theory of relativity (the second effect having never before been directly measured):

1. The geodetic effect—the amount by which the Earth warps the local spacetime in which it resides.
2. The frame-dragging effect—the amount by which the rotating Earth drags its local spacetime around with it.

The GP-B experiment tests these two effects by precisely measuring the displacement angles of the spin axes of the four gyros over the course of a year and comparing these experimental results with predictions from Einstein's theory.

GP-B is actually the second dedicated NASA physics experiment to test aspects of general relativity. The first, Gravity Probe A, was led in 1976 by Dr. Robert Vessot of the Smithsonian Astrophysical Observatory. Gravity Probe A compared elapsed time in three identical hydrogen maser clocks—two on the ground and the third traveling for two hours in a rocket, and confirmed the Einstein redshift prediction to 1.4 parts in 10⁴.

Why Perform Another Test of Einstein's Theory?

With the general theory of relativity, acclaimed as one of the most brilliant creations of the human mind, Einstein forever changed our Newtonian view of gravity. However, even though it has become one of the cornerstones of modern physics, general relativity has remained the least tested of Einstein’s theories. The reason is, as Caltech physicist Kip Thorne once put it:

“In the realm of black holes and the universe, the language of general relativity is spoken, and it is spoken loudly. But in our tiny solar system, the effects of general relativity are but whispers.”

And so, any measurements of the relativistic effects of gravity around Earth must be carried out with utmost precision. Over the past 90 years, various tests of the theory suggest that Einstein was on the right track. But, in most previous tests, the relativity signals had to be extracted from a significant level of background noise. The purpose of GP-B is to test Einstein’s theory by carrying out the experiment in a pristine orbiting laboratory, thereby reducing background noise to insignificant levels and enabling the Probe to examine general relativity in new ways.

Gravity is the most fundamental force in nature; it affects all of us all the time. But, gravity is still an enigma—we don’t completely understand it. Einstein’s 1916 general theory of relativity forever changed our notions of space and time, and it gave us a new way to think about gravity. If the Gravity Probe-B experimental results corroborate the geodetic and frame-dragging predictions of general relativity, we will have made the most precise measurement of the shape of local spacetime, and confirmed the theory of general relativity to a new standard of precision. If on the other hand, the results disagree with Einstein's theoretical predictions, we may be faced with the challenge of constructing a whole new theory of the universe’s structure and the motion of matter.

Such rigorous experimental verification is essential to furthering our understanding of the nature of our universe, particularly about massive objects in space, such as black holes and quasars. As GP-B Physicist John Mester notes:

“General relativity is our current theory of gravitation, and it has wide-ranging implications for our understanding of the structure of the cosmos. At present, Einstein’s theory of gravitation lies outside the other three forces of nature (the strong force, the weak force and the electromagnetic force), which are explained within a unified framework called "The Standard Model." Attempts to unify all four forces of nature have eluded physicists from Einstein to the current day. Testing theories to high precision will help define their range of validity or reveal where these theories break down.”

Whatever the result, Gravity Probe B has provided us another glimpse into the sublime structure of our universe.

The Geodetic and Frame-Dragging Effects

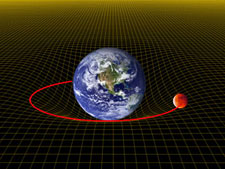
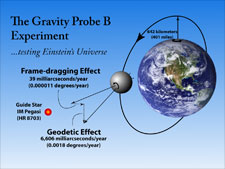
Gravity Probe B was designed to test, through a direct, controlled experiment, two predictions of Einstein’s general theory of relativity. The first, known as the geodetic —or as it is sometimes called, deSitter— effect, measures the size of the very small angle by which our Earth warps its local spacetime. One way to visualize this effect is to think of local spacetime as a trampoline and the Earth a bowling ball lying in the middle. The heavy ball warps or puts a dent in the trampoline, so that a marble (another celestial body) moving along the trampoline surface will be inexorably drawn down the warped slope towards the massive ball.

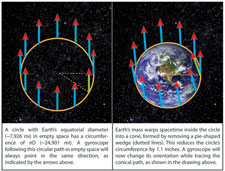
An alternative way to visualize the geodetic warping of spacetime is the so-called “missing inch” shown in the diagram and video clip below. If you were to draw a circle with the same diameter (D) as the Earth (~7,900 miles) in empty space, the circumference of this circle, calculated using standard Euclidian geometry, would be π x D (~24,000 miles). Furthermore, a gyroscope following this circular path in empty space would always point in the same direction, as illustrated in the left side of the diagram.

Diagram of the "missing inch" caused by the geodetic warping of spacetime around Earth	Physicist Kip Thorne explains the "missing inch" during the GP-B pre-launch press conference.

However, if you were then to slip the Earth inside this circle, Earth’s mass warps the spacetime inside the circle into a shallow cone, thereby shrinking the circumference of the circle by a mere 1.1 inches. You can see this effect (not to scale) by cutting out a pie-shaped wedge from the circle and then closing the gap. The circumference of the resulting cone is slightly diminished, and the orientation of a gyroscope will now shift as it moves around the circular edge of the cone, as shown in the right half of diagram. Measuring this shifting orientation of a gyroscope’s spin axis as it moves through warped spacetime is the essence of the GP-B experiment.

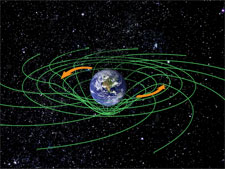
The other effect being measured by GP-B, known as “frame-dragging,” was postulated by Austrian physicists Josef Lense and Hans Thirring two years after Einstein published his general theory of relativity. It states that as a celestial body spins on its axis, it drags local spacetime around with it, much like a spinning ball in bowl of molasses would drag around some of the molasses as it spins. This concept is illustrated in the diagram to the right.

Particularly intriguing, the frame-dragging measurement probes a new facet of general relativity—the way in which spacetime is dragged around by a rotating body. This novel effect closely parallels the way in which a rotating electrically charged body generates magnetism. For this reason it is often referred to as the “gravitomagnetic effect,” and measuring it can be regarded as discovering a new force in nature, the gravitomagnetic force.

Experimental Design

Conceptually, the GP-B experiment is simple:

Animation showing the conceptual
simplicity of GP-B

1. Place a gyroscope and a telescope in a polar-orbiting satellite, 642 km (400 mi) above the Earth. (GP-B actually uses four gyroscopes for redundancy.)
2. At the start of the experiment, align both the telescope and the spin axis of each gyroscope with a distant reference point—a guide star.
3. Keep the telescope aligned with the guide star for a year, as the spacecraft makes over 5,000 orbits around the Earth, and measure the change in the spin-axis alignment of each gyro over this period in both the plane of the orbit (the geodetic precession) and orthogonally in the plane of the Earth's rotation (frame-dragging precession).

The predicted geodetic gyro-spin-axis precession is a tiny angle of 6,606 milliarcseconds (0.0018 degrees) in the orbital plane of the spacecraft. The orthogonal frame-dragging precession is a minuscule angle of 39 milliarcseconds (1.1x10^-5 degrees).

The goal of the GP-B experiment is to measure the geodetic effect to an accuracy of ~0.01%, and to measure the frame-dragging effect, which has not previously been directly measured, to an accuracy ~1%.

Seven "Near Zeroes"

Designing a physics experiment involves a basic choice: maximize the effect to be measured, or minimize the “noise” that obscures it. For the Gravity Probe-B experiment, that choice was moot because Einstein's relativistic effects that literally “roar” near black holes whisper almost inaudibly here on earth. Thus, implementing the experimental design described above required meeting seven near-zero design constraints—three near-zero constraints on the gyro rotors, which had to be near-perfect spheres, with uniform superconductive coatings and virtually no imperfections in shape and density, and four near-zero constraints on the pristine space-borne, cryogenic laboratory, which housed the gyros and shielded them from any sources of noise or interference that might distort the results—solar radiation, atmospheric friction, magnetic fields, electro-magnetic signals radiating from Earth, and so on. The table below summarizes these seven near-zero constraints, showing the tolerance required and the tolerance actually achieved for each one during the mission.

Experimental Variable	Tolerance Requirements	Tolerances Achieved During Mission
Gyroscope Rotor Near Zeros
Mechanical Sphericity	50 nanometers (2 micro inches)	<10 nanometers (< 0.4 microinches)
Material Homogeneity	3 parts in 106	3 parts in 107
Electrical Sphericity	5 parts in 107	<5 parts in 107
Probe Environment Near Zeros
Temperature	1.95 kelvin (-271.2° Celsius or -456.2° Fahrenheit)	1.8 kelvin (-271.4° Celsius or -456.4° Fahrenheit)
Non-Gravitational Residual Acceleration	Less than 10-10 g	Less than 5 x 10-12 g
Background Magnetic Field	10-6 gauss	Less than 10-7 gauss
Probe Pressure	10-11 torr	Less than 10-11 torr

Astrophysical Significance of the GP-B Experiment

Physics advances experimentally in two ways:

1. Measuring known effects with higher accuracy
2. Investigating previously untested phenomena

The geodetic effect has previously been determined to ~1% in complex studies of the Earth-Moon system around the Sun. GP-B aims to measure it to ~0.01%. The frame-dragging effect, on the other hand, is so minuscule around a planet the size of our Earth that until GP-B, it has not been possible to measure this effect directly. However, the frame-dragging effect is of particular interest to physicists and cosmologists who study black holes, because like the air in a hurling tornado, the hurling space around a black hole has enormous destructive potential.

At the GP-B press conference held at NASA Headquarters in April 2004, just prior to the GP-B launch, Caltech physicist Kip Thorne, one of the world’s leading experts on black holes, made the following comments on the significance of the frame-dragging effect:

“The black dot in the center [drawing in the video clip to the right] represents a black hole. It is surrounded by an accretion disc of gas, shown in yellow, that we believe is forced into the equatorial plane of the black hole by the dragging of spacetime in that vicinity. Jets of energy [blue light in the video clip drawing] shoot out in both directions along the spin axis produced by frame-dragging around the black hole. Furthermore, the interaction of the frame-dragging around black holes with magnetic fields is responsible for the enormous and destructive power generation that produces the jets of energy streaming out of these objects.”

Thorne then concluded:

“The results of the GP-B experiment will enable us to verify that the frame-dragging effect does indeed exist, and that it is directly proportional to the angular momentum of our spinning Earth. Physicists and cosmologists will then be able to extrapolate these frame-dragging measurements around the Earth to much more massive celestial objects, such as black holes and quasars.”

Note: For a more in-depth discussion, read Kip Thorne's paper entitled, Gravitomagnetism, Jets in Quasars, and the Stanford Gyroscope Experiment, in the book, Near Zero: New Frontiers of Physics, ed. J. D. Fairbank et. al., New York, W. H. Freeman, 1988.

History & Management (Next) ->